Quantum Optics, Cavities and Molecules
The study of strong light-matter interactions is playing an increasingly crucial role in understanding as well as engineering new states of matter with relevance to the fields of quantum optics, quantum information, solid state physics, quantum chemistry and material science.
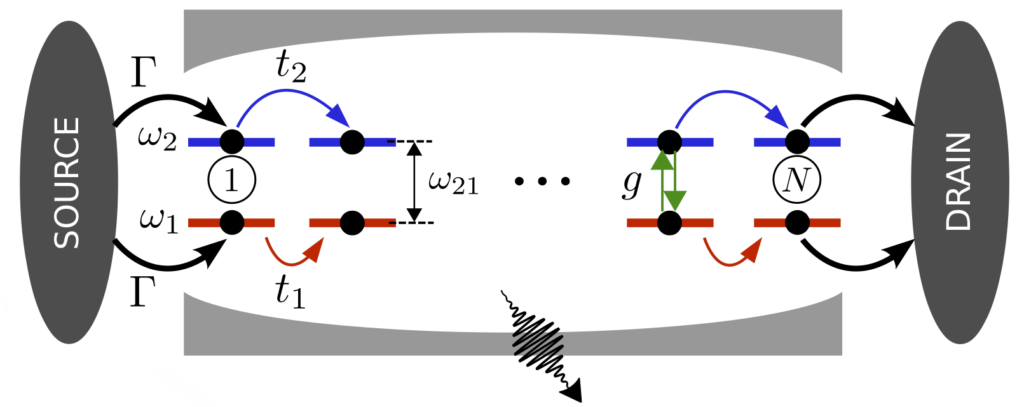
We are particularly interested in investigating how light-matter interactions can enhance transport properties of excitons and charge in molecular semi-conductors for basic science and quantum technologies.
For example, in recent publications we have provided and analyzed possible theoretical mechanisms that can lead to an enhanced charge conductivity mediated by the vacuum of a surrounding cavity mode with important implications for current experiments in Strasbourg.
In the case of “strong coupling” of the system to a cavity mode, the energy exchange between matter and the photonic mode can become faster than the rates of dissipative loss mechanisms. In such a case “polaritonic states”, i.e. hybrid states between light and matter become crucial to the system dynamics. We have shown that states can lead to dramatically modified energy conduction properties of materials.
From few-particle interactions to quantum gases, fluids and solid
We are interested in the design of inter-particle atomic and molecular interactions at cold and ultracold temperatures using quantum optical techniques and the investigation of many-body quantum phenomena resulting from these interactions in cold gases. Recent interests include:
- long-range interactions with Rydberg atoms, dipolar atoms, polar molecules, cold ions
- supersolids, superglasses
- topological models of fermions
- disordered quantum phases
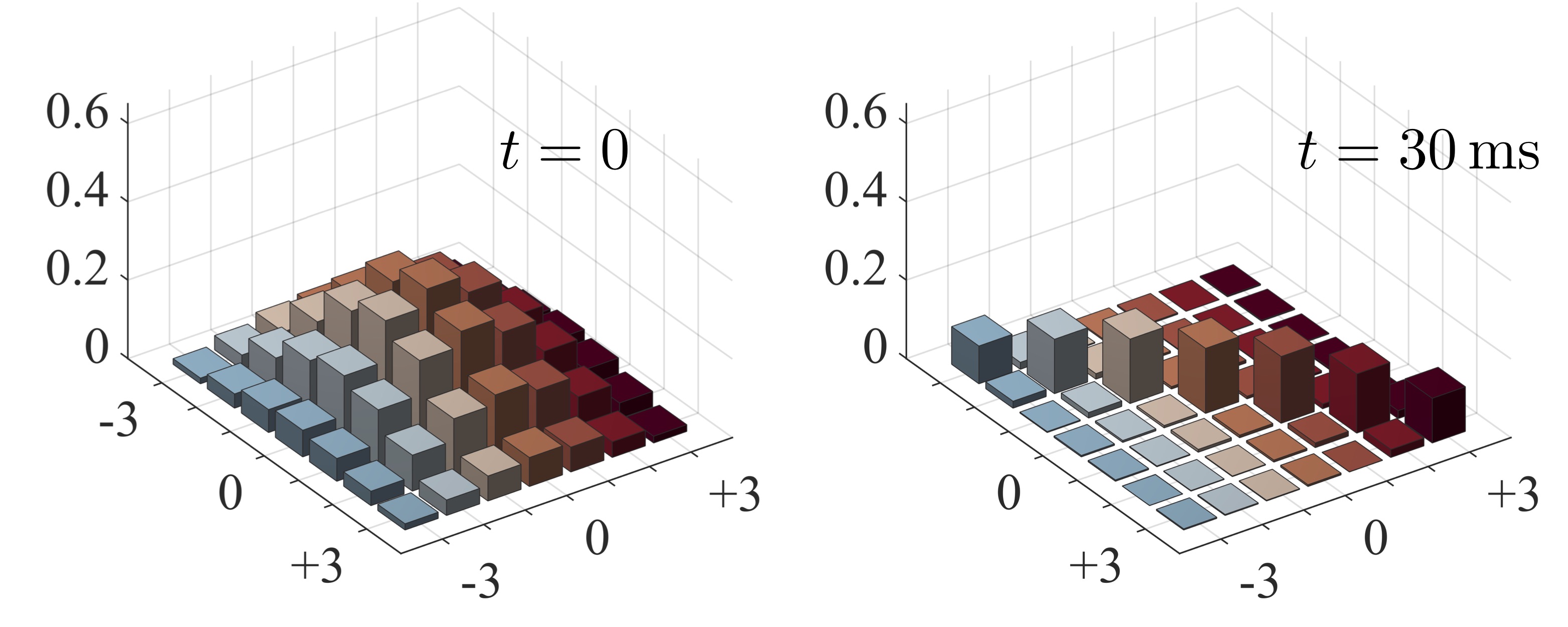
Besides exotic equilibrium states of matter, we’re also particularly interested in non-equilibrium dynamics of many-body quantum models. For example, recently we were involved in modeling the entanglement build-up and thermalization of ultra-cold Chromium atoms, trapped in an optical lattice and interacting via magnetic long-range dipolar interactions (Experiments at the Cold atoms group, LPL, Paris).
Numerical methods in Many-Body Quantum Physics
We utilize and develop advanced theoretical techniques for the numerical solution of the many-body problem in closed and open quantum systems. These include:
- Path-Integral Quantum Monte-Carlo
- Density-Matrix Renormalization Group methods (DMRG)
- time-dependent matrix product state methods (t-DMRG/TEBD)
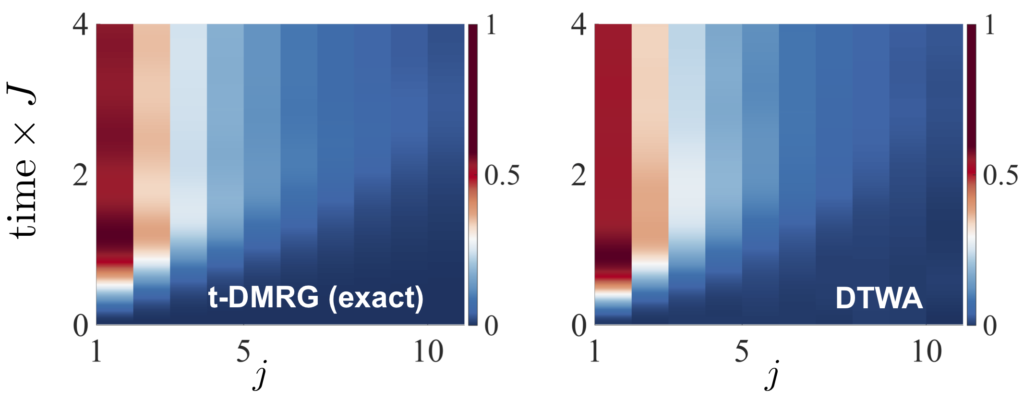
- Semiclassical discrete truncated Wigner approximation
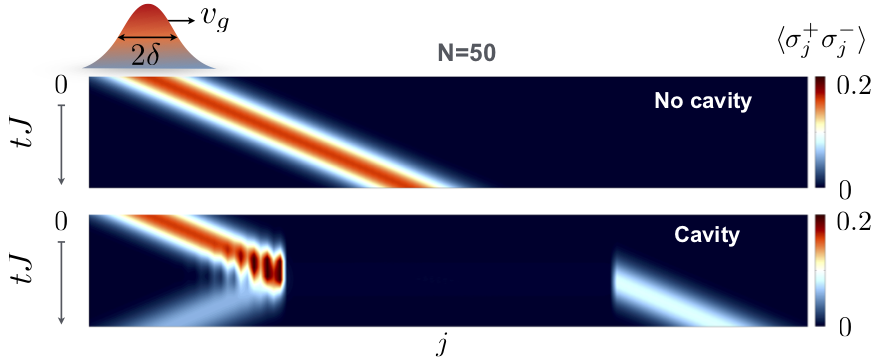
Density matrix renormalization group methods and its time-dependent versions are excellent tools to simulate equilibrium & non-equilibrium physics in low dimensional geometries. Their success relies on an efficient representation of many-body quantum states in terms of so-called matrix product states (MPS). Such MPS can be a quasi-exact representation of a full many-body quantum state in cases of limited amount of quantum-correlations/entanglement. We can use these concepts to study, for example, dynamics of correlations in long-range interacting spin-models.
To study dynamics for large sytems also in 2D or 3D configurations we use new adaptations of semi-classical phase-space methods (such as the DTWA), which has proven to be remarkably accurate in many situations.